Numerical Estimation of the Largest Lyapunov Exponent of Pluto’s Orbit

For the final project of a dynamical systems course I took in Spring 2014, I recreated some existing results¹ on whether Pluto’s orbit is chaotic. To do this, I sought to estimate the largest Lyapunov exponent of Pluto’s orbit. If the estimated exponent is positive, that is an indication that the orbit is chaotic.

In my senior thesis, I wrote MATLAB code that implemented a low-order symplectic integrator for the orbit of the outer planets plus Pluto. Perhaps fortunately the MATLAB code was painfully slow to run, especially with my modifications for the Lyapunov exponent estimation. So I ported it to Fortran, which gave a healthy 130x speedup.

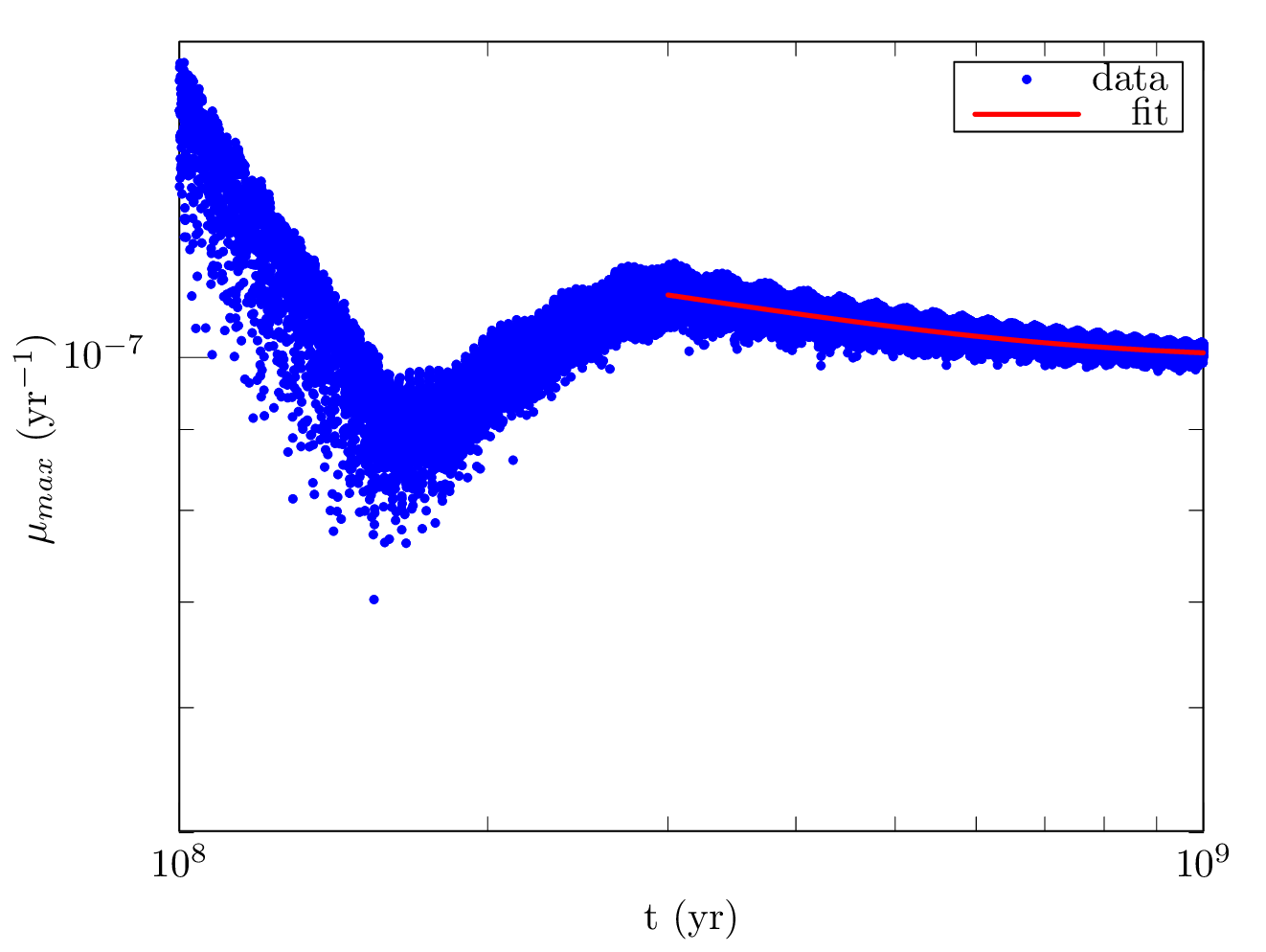
Porting to Fortran allowed the code to run fast enough on my laptop for me to estimate the Lyapunov exponent in a tolerable amount of time. The figure below shows the convergence of the largest Lyapunov exponent. I fit a decaying exponential to estimate the value to which it appears to converge, giving an estimated exponent of \(10^{-7.0} /\textrm{yr}\), which is close to prior estimates¹. Here is my final report for the project, which gives many more details.

---

1. G. Sussman and J. Wisdom, Numerical evidence that the motion of Pluto is chaotic, Science, (1988). ↩ ↩²